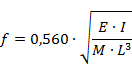|
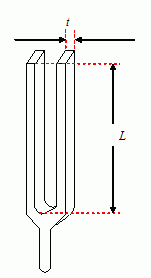
Hvad er dimensionerne på en stemmegaffel og hvordan svinger den? I pricippet består en stemmegaffel af 2 stænger, som er fastspændt i den ene ende og frie i den anden ende. Når stemmegaflen afslås, opstår en stående bølge med knude nederst og bug ved de frie ender. Grenene svinger mod hinanden eller fra hinanden. Derfor bevæger skaftet sig opad, når grenene bevæger sig udad og nedad, når grenene bevæger sig indad.
|
 |
En stang fastspændt i den ene ende svinger med frekvensen,
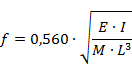
Hvor E er youngs modul, I er arealmomentet. M er massen og L og længden.
Arealmomentet for en
stang er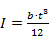 
, hvor b er bredden og t er
tykkelsen af stangen.
Desuden er
lydhastigheden i metallet bestemt ved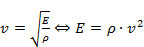 
, hvor r
er densiteten.
Indsættes udtrykket for hastighed v og arealmoment I i formlen for frekvensen f, fås:
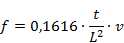
Hvor er t er tykkelsen, L er længden og v er hastigheden i metallet.
Hastigheden bestemmes nu ved at måle længde L, tykkelse t og frekvens f for en række stemmegafler og afbilde f som funktion af t/L2 .
L måles med skydelære. t med skydelære eller mikrometerskrue, f måles ved fourrieranalyse i Datalyse vha af lydkort og mikrofon.
Skema:
|
f / Hz |
t venstre gren / mm |
t højre gren / mm |
t snit / mm |
L / mm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bestem herefter hastigheden vha. tendenslinjens hældning.
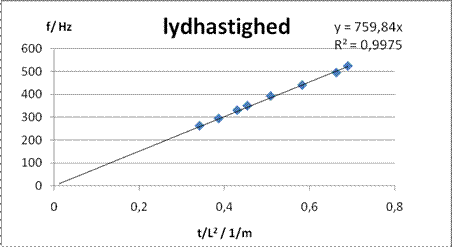
Lydhastigheden i metallet bliver v = 4700 m/s.
Forsøget kan bruges på alle niveauer. Men udledningen af formlen for frekvensen indebærer løsning af en 4 ordens differentialligning. Det kunne være et emne til en studieretningsopgave.
Men selve eftervisningen af formlen er god, for vi har ikke så mange forsøg, hvor der skal måles med skydelære.
En stemmegaffel har også overtoner. Forholdet mellem tonerne er:
1,1942, 2,9882, 52, 72, … (2n-1)2,…
Spektrum af en stemmegaffel med frekvensen f =288 Hz. Der ses to overtoner.
Link: http://www.ikhebeenvraag.be/mediastorage/FSDocument/137/Tuning+Fork+Physics+Teacher.pdf
